บทความ

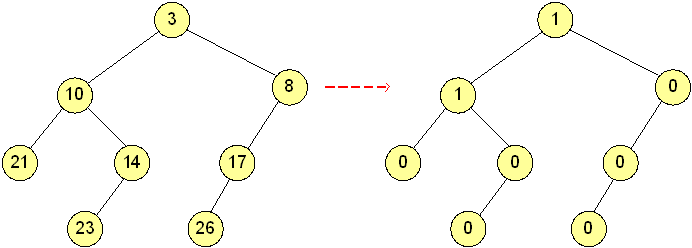
การหมุนต้นไม้ เพื่อให้คงสภาพ Balance Tree (AVL Tree)

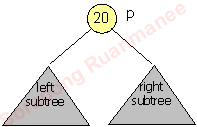
รูปภาพ
การหมุนเพื่อคงสภาพ AVL Tree สมมุติต้นไม้ Binary Search Tree ขึ้นมา 1 ต้น ที่อยู่ในสภาพ balance และสมมุติโหนด p เป็นโหนดที่อาจจะต้องถูก rebalance เนื่องมีโหนดใหม่ถูกเพิ่มเข้ามาเป็นลูกของ subtree ด้านซ้าย หรือ subtree ด้านขวา เช่น ถ้าสมมุติ Binary Search Tree ไว้ดังภาพนี้ เราจะต้องทำการ rebalance ก็ต่อเมื่อ Height ด้านซ้ายของ p แตกต่างจาก Height ด้านขวาของ p มากกว่า 2 เช่นแบบนี้ แต่ถ้าความสูง (height) แตกต่างกันน้อยกว่า 2 (เช่น 0 หรือ 1) เราจะไม่ต้องทำการ rebalance เพราะฉะนั้นกรณีที่จะทำให้เราต้อง rebalance โหนด p มีอยู่ 4 กรณีคือ กรณี 1 เพิ่มโหนดใหม่เข้าไปที่ subtree ด้านซ้าย ของโหนดลูกด้านซ้ายของ p ( สมมุติ n เป็นโหนดใหม่) กรณี 2 เพิ่มโหนดใหม่เข้าไปที่ subtree ด้านขวา ของโหนดลูกด้านซ้ายของ p กรณี 3 เพิ่มโหนดใหม่เข้าไปที่ subtree ด้านซ้ายของโหนดลูกด้านขวาของ p กรณี 4 เพิ่มโหนดใหม่เข้าไปที่ subtree ด้านขวาของโหนดลูกด้านขวาของ p ทั้ง 4 กรณีนี้อาจจะทำให้ length ด้านซ้ายมีความยาวต่างกับ length ด้านขวาเท่ากับ 2 ก็ได้ แต่กรณีที่ 1
แสดงความคิดเห็น
อ่านเพิ่มเติม

Leftist Heap

รูปภาพ
Leftist Heap วิธีการนับ null path length (npl) ก็คือ โหนดไหนไม่มีลูก หรือ มีลูกแค่ 1 ตัว เราให้ npl = 0 ส่วนโหนดมีลูกครบ 2 ตัว เราให้ npl = 1 ตัวอย่างการหาค่า npl ของ Heap ต่อไปนี้ เมื่อนับค่า npl ได้แล้ว เราจะตัดสินใจว่า Heap ไหนเป็น Leftist Heap โดยใช้กฏว่า “ ทุกๆโหนดใน Heap ลูกด้านซ้ายต้องมีค่า npl มากกว่าหรือเท่ากับ ลูกด้านขวาเสมอ ” ถ้ามีโหนดใน Heap ฝืนกฏนี้ถือว่า Heap นั้นทั้งตัวไม่เป็น Leftist Heap ตัวอย่างของ Heap ที่เป็น Leftist และที่ไม่เป็น ดังภาพต่อไปนี้ ในภาพข้างบนนี้เป็น Leftist Heap เนื่องจากทุกๆโหนดใน Heap มีค่า npl ของลูกด้านซ้ายมากกว่าหรือเท่ากับลูกด้านขวาทั้งหมด (คือไม่ 1-0 ก็ 0-0 ถือว่าใช้ได้ แต่ถ้าเจอ 0-1 ถือว่าผิดกฏ) ภาพนี้ Heap ไม่เป็น Leftist เพราะมีโหนดที่ฝืนกฏ โดยมี npl ของลูกด้านซ้ายเป็น 0 และ npl ลูกด้านขวาเป็น 1 ดังนั้นทั้ง Heap นี้ไม่เป็น Leftist Merge Leftist Heap เนื่องจาก Leftist Heap ทำมาไว้เพื่อให้การจับ Heap 2 ตัวมารวมกัน ทำได้ง่าย โดยใช้หลักการดังนี้ สมมุติว่ามี Leftist Heap 2 ตัว คือ H1 และ H2 o     ให้ Root ขอ
แสดงความคิดเห็น
อ่านเพิ่มเติม

Huffman's Code

รูปภาพ
Huffman’s Code สมมุติว่าเราต้องการบีบอัดไฟล์ข้อมูล (compression) เช่นพวก zip ไฟล์ ปกติแล้วเราจะเปลี่ยนตัวอักษรที่อยู่ในไฟล์ให้กลายเป็นบิตข้อมูล (bit) ที่มีขนาดเล็กกว่าบิตข้อมูลธรรมดา เช่น ปกต ิเลข 5 อาจจะเป็นตัวเลข 0000 0101 ถ้าเก็บแบบ 8 บิต แต่ถ้าเราบีบอัดแล้วอาจจะใช้ที่เก็บจริงๆแค่ 3 บิตคือ 101 เท่านั้น เช่นถ้าในไฟล์เรามีข้อมูลตัวอักษร a, e, i, s, t, space bar, new line (สำหรับ space bar ก็คือช่องไฟ และ new line คือ ขึ้นบรรทัดใหม่ พวกนี้เป็นตัวอักษรล่องหน มองไม่เห็น แต่กินพื้นที่ไฟล์ด้วยเช่นกัน) เราต้องการบีบอัดไฟล์นี้ให้มีขนาดเล็กเราอาจจะเปลี่ยนตัวอักษรเหล่านี้ให้กลายเป็นรหัสขนาด 3 บิต ดังตารางต่อไปนี้ จากตารางข้างต้น สมมุติว่าในไฟล์มีข้อมูลดังนี้ aaeeiiissttt  a  ti เราสามารถแปลงให้กลายเป็นรหัสตามที่กำหนดไว้ได้ดังนี้ 000 000 001 001 010 010 010 011 011 100 100 100 110 000 101 101 100 010 เมื่อนับจำนวนบิตดูจะพบว่ามีขนาดทั้งหมด เท่ากับ 18 x 3 = 54 บิต สมมุติว่าถ้าในไฟล์มีตัว a อยู่ 10 ตัว ตัว e อยู่ 15 ตัว ตัว i อยู่ 12 ตัว ตัว s อยู่ 3 ตัว ตัว t อยู่ 4 ตั
2 ความคิดเห็น
อ่านเพิ่มเติม